Standsicherheitsgefährdende Erschütterungen
Statische und dynamische Lasten
Bauwerke werden gegen statische, d.h. über die Zeit konstante Einwirkungen ausgelegt. Das bedeutet, dass das gesamte Bauwerk sowie seine tragenden Bauteile so dimensioniert werden müssen, dass sie die Lasten aus diesen Einwirkungen abtragen können und somit standsicher bleiben. Eine statische Last, die jedes Bauwerk tragen muss, ist sein Eigengewicht.
Neben den statischen, d.h. zeitunabhängigen Lasten gibt es aber auch eine Reihe von zeitabhängigen Lasten, die auf Bauwerke einwirken. Diese dynamischen Lasten müssen ebenso durch das Tragwerk des Gebäudes abgetragen werden.
Solche dynamische Lasten entstehen beispielsweise aus
- Verkehr
- Maschinenbetrieb
- menschlichen Bewegungen
- Wind
- Wellen
- Anprall
- Explosion
- Erdbeben
Die Palette von Bauwerken, die gegen dynamische Lasten ausgelegt werden, reicht von Ingenieurbauwerken wie Brücken, Türmen, Tunneln und Hochhäusern über bauliche Anlagen der Energiegewinnung und/oder hohem Risikopotenzial, wie Kernkraftwerke, Chemie- und Windkraftanlagen, bis hin zu gewöhnlichen Wohnhäusern.
Genau genommen sind alle denkbaren Belastungen, welche auf ein Bauwerk einwirken, zeitabhängig also dynamisch. Selbst das Eigengewicht wird zu einem gewissen Zeitpunkt (dem der Herstellung des Bauteils) aufgebracht und ist damit zeitabhängig. Der wesentliche Unterschied zu den zuvor erwähnten dynamischen Lasten ist, dass die Auswirkungen der Massenträgheit bei den so genannten statischen Lasten vernachlässigt werden kann. Bei den dynamischen Einwirkungen spielen hingegen die Einflüsse aus Massenträgheit und Dämpfung die entscheidende Rolle.
Bauwerksauslegung gegen dynamische Lasten
Der zeitliche Ablauf oder der genaue Ort des Auftretens einer dynamischen Lastgröße ist oftmals unbekannt oder variabel. Beispielsweise ist bei einer Decke in einem Wohnhaus im Vorhinein nicht bekannt, wie viele Leute sie überqueren, welchen Weg sie dabei einschlagen, mit welcher Geschwindigkeit sie gehen, ob sie stehen bleiben oder hüpfen, usw.. Aber auch bei wesentlich größeren Lasten, wie beispielsweise Erdbeben oder Lasten aus Flugzeugabsturz, wird oftmals eine einhüllende Betrachtung über mehrere möglich Szenarien unter probabilistischen Gesichtspunkten gemacht. So decken beispielsweise die Lastannahmen einer normgerechten Erdbebenauslegung eine Vielzahl von möglichen Erdbeben ab. Die dynamischen Lastvorgaben sind daher meist als Einhüllende mehrere dynamischer Lastfälle zu verstehen.
Dynamische Lasten werden bei der Auslegung von Bauwerken nur teilweise auch tatsächlich als zeitabhängig berücksichtigt. Stattdessen werden oftmals vereinfacht statische Ersatzlasten für die Auslegung von Bauwerken verwendet. Dazu müssen die dynamischen Lasten, welche auf eine Baustruktur wirken, in äquivalente statische Lasten umgewandelt werden.
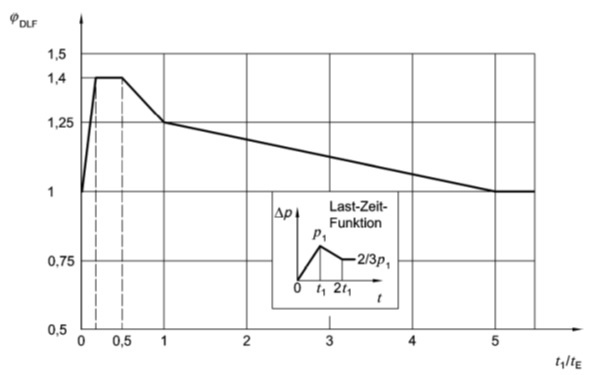
Durch die alleinige Berücksichtigung des Maximalwerts der zeitlich veränderlichen Last wird aber das dynamische Verhalten, also die Auswirkungen von Massenträgheit, Dämpfung, etc. nur unzureichend erfasst. Durch die erwähnten dynamischen Effekte kann es zu Vergrößerungen aber auch zu Reduktionen der zur dynamischen Belastung äquivalenten statischen Last kommen. Für eine adäquate Berücksichtigung des Verhaltens einer durch eine dynamische Einwirkung belastete Struktur reicht es daher nicht aus den Maximalwert des zeitlichen Verlaufs der Last als statische Belastung zu verwenden. Vielmehr ist es notwendig diesen Maximalwert noch mit einem sogenannten dynamischen Lastfaktor zu multiplizieren. Dieser dynamische Lastfaktor beinhaltet den dynamischen Anregungscharakter einer individuellen Last in Abhängigkeit des Schwingverhaltens der belasteten Baustruktur.
Das Bild zeigt exemplarisch für eine Explosiusdruckwellenbelastung den Verlauf des dynamischen Lastfaktors in Abhängigkeit der Schwingperiode.
Wichtig ist also, dass nicht nur der zeitabhängige Verlauf der Last sondern auch das Schwingverhalten der belasteten Struktur eine Rolle bei der dynamischen Auslegung von Baustrukturen spielt. Dem Verhältnis der Anregungsfrequenz der Last und der Antwortfrequenz der belasteten Baustruktur kommt dabei eine entscheidende Bedeutung zu. Liegen die beiden Frequenzen nah beieinander, stellt sich ein so genannter Resonanzeffekt ein, durch welchen sich die Belastung der Struktur um ein Vielfaches des Maximalwertes der Last vergrößern kann.
Die Kenntnis der wesentlichen Frequenzen der Anregung ist daher auch Voraussetzung für Modellbildung des von der dynamischen Einwirkung belasteten Systems. Bei niedrigen Anregungsfrequenzen, wie z.B. bei Erdbeben oder Wind, können ganze Gebäude in Schwingung versetzt werden, während bei hochfrequenten dynamischen Lasten, beispielsweise bei stoßartigen Anprallbelastungen, zusätzlich lokale Phänomene im belasteten Bauteil von Bedeutung sind.
Das Zusammenspiel von dynamischer Anregung und dynamischem Antwortverhalten der Baustruktur muss also in der Modellabbildung berücksichtigt werden. Dabei kann es sein, dass in Abhängigkeit des interessierenden Phänomens unterschiedliche Modelle für denselben Lastfall zur Anwendung kommen. Trifft beispielsweise ein Flugzeug eine Stahlbetonwand treten hochdynamische Effekte in einem lokal eng begrenzten Gebiet auf. Soll eine Bauteilauslegung für den unmittelbar getroffenen Bereich erfolgen, wird ein detailliertes Modell dieses lokalen Bereichs benötigt. Gilt es hingegen die Standsicherheit des gesamten Gebäudes zu gewährleisten, spielen Phänomene im niedrigeren Frequenzbereich eine Rolle und ein hoher Detaillierungsgrad des Auftreffortes ist nicht notwendig. Anstelle dessen müssen die wesentlichen dynamischen Eigenschaften des gesamten Gebäudes modelliert werden.